In order that vision may be distinct, it is necessary that the rays should enter the eye in the direction of what is termed the visual axis, and the various movements of the organ tend unceasingly to place it in a position to fulfil this condition, and it is necessary, also, that the light should be neither too strong nor too weak, and that the rays shall traverse the central portion only of the crystalline, and not its borders. In order to obtain an analogous result in some of their instruments, opticians divide them by means of a partition pierced by a hole in the centre, which is termed a diaphragm. We find a similar arrangement in the eye, " an intelligent diaphragm," to use the expression of M. Longet, that is the iris, which dilates or contracts the pupil in such a manner as to measure the quantity of light necessary to vision, and which only allows those rays to pass which are directed toward the central portion of the crystalline lens. In the dark, or if we look at an object but slightly illuminated, the pupil dilates in order to admit the greatest possible number of rays which are refracted by the cornea; it is the same if we look at a distant object, the rays from which are less divergent; if this object becomes more luminous, or if we approach it, the pupil contracts in proportion.

Optic centre, visual angle, appreciation of the size of obJects. —The rays emanating from two points of an object, p h (fig. 38), converge toward the optic centre o, at a point in the eye a little behind the crystalline, and thus form an angle p o h, which is called the visual angle. From the optic centre these rays diverge to the retina, and form an angle, p o h, equal to the first, the base of which, corresponding to the retina, measures the size of the image which they form upon it. The visual angle therefore gives us an idea of the size of objects, and enables us to compare them, but in order that our ideas may be exact, they must be confirmed by our notions of distance. In fact, several objects of unequal size, p h, p' h', p"h", may be placed at such distances, a b c (fig. 38), as to subtend the same visual angle; we must therefore estimate their relative distance, in order to judge correctly of their size. We can also obtain a knowledge of their size, if we know that of any portion of the object which we see, or the size of another object placed at an equal distance. Thus, when we look at a ship at sea, we can judge of its size by that of the men whom we see upon it; the height of a balustrade enables us to calculate approximately that of the building of which it forms a part. When the means of comparison fail us, it is very difficult to avoid errors, the very causes of which escape us. Thus, the sun and the moon when they are near the horizon, seem to present a much greater diameter than when high in the heavens. The atmosphere causes objects to appear near or distant, according as it is pure, or charged with mist These illusions are frequent, especially among mountains, and the inexperienced traveller should not count too much upon the exactness of his impressions.

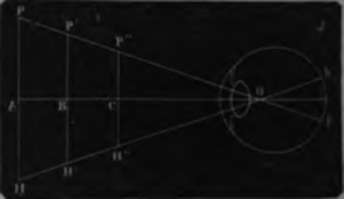
Fig. 33.

Bravais points out a very common error in drawing a rough hill-side in relief, or a mountainous horizon. In verifying a sketch mathematically, the horizontal distances of the different points in the landscape are found to be sufficiently exact, while the height of the summits, or of inequalities of surface, is in double proportion. But we must add, that the design adjusted mathematically seems incorrect in an opposite sense, and does not give the impression of the natural relief.

If a rainbow is formed over a cascade when the sun is near the horizon, and the circle of this bow is nearly complete, we seem to see not a circle, but an ellipse, of which the principal axis is vertical; the same illusion is produced when we look at a halo.