Hittorf's Migration Constants
Description
This section is from the book "Modern Chemistry", by William Ramsay. Also available from Amazon: Modern Chemistry: Theoretical and Modern Chemistry (Volume 2).
Hittorf's Migration Constants
The fact that ions move at different rates can be demonstrated in two ways, one direct, the other indirect. The indirect method was devised by Hittorf; the direct method, which is much more recent, was first suggested by Lodge.
It is always advisable to form a mental picture, if possible, of any physical phenomenon, pour preciser les idees, as the French say ; and a trivial illustration will be now given which may render Hittorf s conception clearer. Imagine a ball-room with a door at each end. Suppose the partners to be all separated from each other ; and suppose an order to be given that the men shall march to one door at twice the rate at which the ladies make for the other door; but that at the same time, for every man who passes through the one door, only one lady shall pass through the other door. At a given signal, say when half the ballroom has escaped, let the condition of the room be examined. It is easy to see that there will be an equal number of men and women in the room, but that there will be a greater number round the door at which the men issue than round that at which the ladies are trying to escape. And the rates of motion will be proportional to the relative numbers in each half of the ballroom, for the greater the rates at which the men move proportionally to the ladies, the greater will be the number in that part of the room at which the men are escaping.
This is a conception in close analogy with Hittorf s. The men and women are the anions and kations ; and on analysing the solutions round the anode and kathode, he found that the concentration was, as a rule, altered, so that he was forced to conclude that the rate of motion towards the pole at which the concentration was increased was more rapid than that towards the pole at which he found the concentration to be diminished. By comparing the concentrations, too, he calculated the relative rates of motion of the anions and the kations towards the kathode and the anode respectively.
Lodge's direct method has recently been improved by Orme Masson, and very accurate results have been obtained by him. His plan is to trace the rate of motion of the anions by following them up with a coloured anion, such as the copper ion, which is blue, and can be seen, while the rate of motion of the kation is indicated by following it up with a coloured kation : the one he used for this purpose is the chromate ion, which is orange-yellow. The apparatus which Masson employed consisted of two flasks connected together by a narrow tube. This tube is filled with a solution of the salt of which the rate of migration of the ions is to be determined, but in order to prevent diffusion of the liquid, or escape owing to currents produced by differences of temperature, the water in which the salt is dissolved contains enough gelatine to make it set into a jelly when cold. It is found that the gelatine does not appreciably interfere with the motion of the ions. The one flask was charged with a solution of copper chloride, and the anode plate was of copper. The other flask was charged with a dilute solution of a mixture of chromate and bichromate of potassium, and the kathode was of platinum. The connecting tube was filled with a warm solution of the salt to be examined, say potassium chloride, in water containing gelatine, and after it had cooled and set it was placed in position. On passing the current, the potassions migrate towards the kathode, and are followed closely by the blue cuprions, which serve to mark the position of the rearmost of the potassions. The chlorions, on the other hand, migrate towards the anode, followed by the orange-yellow chromations, which reveal their position. The rates can be measured by following the advance of the colour in the tubes. If the ions have equal velocity, as is nearly the case with potassions and chlorions, the meeting-place of the blue and the orange is nearly at the middle of the tube ; but if, as in most other cases, the rates are different, the point of junction will be at one side or other of the middle point of the tube. The distances traversed in the same time give a direct measure of the relative velocities of the anion and kation. Having established this ratio, another salt, say sodium chloride, having a different anion but the same kation, can be employed, and so the relative rates of potassion and sodion may be compared.
The table which follows gives the rates of migration of a few ions compared with that of potassion, which is taken as ioo.
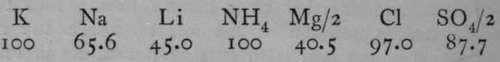 .
.
As the conductivity for a current depends on the velocity both of the anion and the kation, relative numbers for the conductivity may be obtained for any salt by adding the numbers of the individual ions given above. Thus, if it is required to find the conductivity of lithium sulphate, which has the formula Li2SO4, we have Li = 45, and, together equal to 132.7.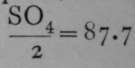 .
.
Continue to:
