Before a lens can be used to advantage certain facts concerning it must be known to the user.

The focus of a very distant point lying on the principal axis of the lens is known as a " principal focus," and every lens has two such principal foci—one, f in fig. 3, for the direct parallel pencil travelling from left to right (in the diagram) and another, f2, for a pencil travelling from right to left. If the object point is brought nearer the lens, say to p, its focus moves in the same direction, from f to q. These two points are called conjugate foci. They are reversible, p being the image of q when q is the object, and the position of each is fixed absolutely by that of the other. When the point p is at one particular distance from f2 the image q is at an equal distance from f, and the distance p f2 or q f is the " focal length " of the lens, which dimension is a most important factor in all calculations relating to the adjustments of the camera.

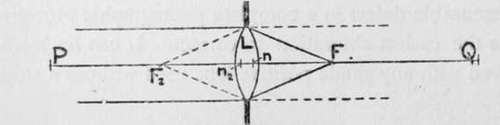
Fig. 3.

If we set out towards the lens distances equal to the focal length from both f and f2, we arrive at two points, n and »2, called " principal points," and while f2 and n2 may be distinguished as the front principal focus and principal point respectively, f and n may be called the back principal focus and point.

The position of object or image may be fixed by its distance either from principal focus or principal point. A measurement from the former point is the extra-focal distance of the object or image, but one from the principal point is distinguished as the focal distance, and a pair of such focal distances are called conjugates. If we multiply a pair of conjugate focal distances together and divide the result by their sum the quotient is the focal length of the lens. This equation represents the " law of conjugate foci," from which we can always find one distance if the other two are known. The extra-focal distances are, however, connected by a simpler rule which is much more easily applied, and of much greater practical use.

Each extra-focal distance is equal to the square of the focal length divided by the other extra-focal distance. Thus the distance p f2 in the fig. is equal to the square of the focal length [divided by q f] (all of course in inches;, while q f is equal to the square of the focal length divided by p f2. Supposing the extra-focal distance of the object, or p f2, to be 10 ft. and the focal length of the lens to be 6 in., then the extra-focal distance of the image, or q f, is 36 in. divided by 120, or three-tenths of an inch. The rule can be thus applied to set the plate at the right distance from the lens when the distance of the object is known. Knowing the extra-focal distance of object or image you can at once arrive at the focal distance by simply adding one focal length. In the above example the focal distance of the object is 10 ft. + 6 in., and that of the image 6 in.+ three tenths of an inch.